The Pareto Distribution: From Intuition to Implementation in Python

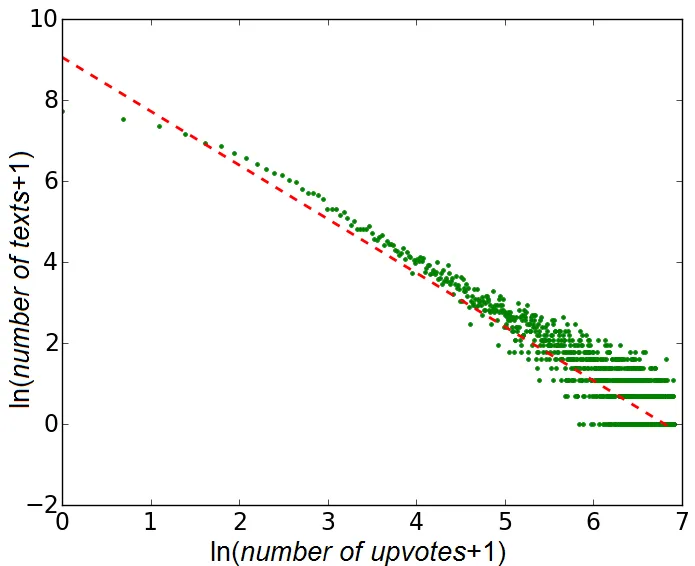
The Pareto distribution is used to model heavy-tailed phenomena where a small number of observations contribute a large share of the total, such as wealth, city sizes, web traffic, or repository popularity. It is especially useful when you care about extreme values in the right tail.

Start by plotting your data on log–log axes and inspecting the survival function or the empirical CDF in the tail. If the tail is roughly a straight line, a Pareto model may be a plausible option. Fit the model, run diagnostics such as Q–Q plots and KS tests, and compare the fit against alternatives like the lognormal.

The shape parameter alpha controls how heavy the tail is. Values just above 1 indicate an extremely heavy tail where the mean exists but is dominated by rare events. For alpha ≤ 1 even the mean does not exist, and for alpha ≤ 2 the variance is infinite. Larger alpha values correspond to lighter tails.

When alpha ≤ 2, the variance of a Pareto distribution is infinite, so variance-based metrics and classical confidence intervals become unreliable. In that regime, it is better to focus on robust statistics, tail quantiles, and risk measures designed specifically for heavy-tailed data.